可口可乐和百事可乐是怎么合作的？

3

　　当你去逛沃尔玛这样的大型超市时，能看到可口可乐和百事可乐在同时促销吗？相信绝大多数人的答案是不。 有人统计发现 在连续的 52 周内，这两个牌子每隔一周进行促销，从不同时促销，也没有哪一周都不促销。与其说这是巧合倒不如说是默契。为什么这种不共戴天的竞争对手也能走到一起？因为没有永恒的敌人。

　　两败俱伤的促销竞争

　　既然不适合做敌人，那一定有不适合的原因。不妨让我们来看看。在任意一周，两家公司的策略无非是促销或者不促销。

　　如果百事和可口可乐都均不促销，设此时收益为 0。若只有百事促销，设它能收益 4，而可口可乐为 -2，这是因为促销不仅能获得更多收益，还吸引了可口可乐消费者中对价格敏感的那部分人。同理，若只有可口可乐促销，则其收益为 4，而百事为 -2。但如果两家公司都促销，原先消费者基本不会改变自己的倾向，两家公司没有额外利润，并且还需要承担促销带来的利润损失，因此收益均为 -1。

　　这看上去就是一个囚徒困境，无论百事选择什么策略，可口可乐肯定都会选择促销。这样一来，百事也就只能选择促销来应对。

　　当然，这样的选择对两家公司来说并不是最优的。由于“被迫”促销，每个厂商都不得不承担让利却不能吸引更多消费者这个他们不想看到的后果，都促销还不如都不促销。而尽管双方都知道这个选择并非最优，也必须仍会坚持选它，因为如果一家选择不促销而另一家促销，就会获益并且让对方承受更大的损失。

　　重复博弈带来的双赢策略

　　要注意的是，他们并非只有一次机会，双方可以多次选择。在连续的两个促销期中，两家公司做出不同选择而导致的收益结果如下表所示。其中 P 表示促销， N 表示不促销。表内数字则分别为可口可乐和百事在不同选择下的收益情况，每个方格中，第一个数字是可口可乐的收益值。

　　对于可口可乐而言，不管百事选择什么策略，他们的最优策略为 PP，因为假设百事等可能地选择 4 种策略，可口可乐选择 PP 所能获得的收益期望就是 （-2 + 3 + 3 + 8） × 0.25 = 3，是 4 种结果里最高的。 类似的，百事的最优策略亦为 PP， 从而得到平衡点如红圈所示。这显然不是双方希望看到的，因为其他所有策略的总收益都比它大。

　　但也有一种双赢的局面，注意到黄圈表示的策略，当两家交替促销时，双方都能收益 2。在多轮促销期的重复中，显然双方谁也不愿一直亏损下去，因此很容易地就转而选择这种双赢的结果。当然，实际上他们并不能聚到一起商量制定一个有利策略，因为这种串通活动可能会把一个存在竞争的市场(这里是寡头市场)变成一个被两家公司平分的垄断市场，而这违反很多国家的法律。虽然对手之间的交流变成了默剧，但谁也和钱没有仇，只要双方都能意识到交替促销最有利，就会化竞争为合作。

2

　　既然可以共存赚钱，那如何确定最优产量以使自己达到利益最大化呢？首先，对于消费者来说，可乐价格越贵，购买量就会越少。因此可以简单地认为价格 p 和可乐总需求 q 呈反比关系（用 p = a - b×q 表示）。为方便起见，我们设市场上只有可口可乐（产量 q 1 ）和百事可乐（产量 q 2 ）两家可乐公司，且他们的产量之和等于消费者对可乐的需求，也就是 q = q 1 + q 2 。假设对于两家公司每罐可乐的成本一样，均为 c，那对于可口可乐来说，其盈利为

　　对 q 1 求导并令其等于 0 即可得到使得可口可乐盈利最大时的产量 q 1 ^= (a - c) / 2b - q 2 / 2。同理能算出百事可乐的最佳产量 q 2 ^ = (a - c) / 2b - q 1 / 2。

　　我们建立一个直角坐标系，横坐标为 q 1 ，纵坐标 q 2 ，然后把两个商家的最优产量随另一个商家产量的变化关系画在一起，得到下面的图。图中标出 Q 1 、 Q 2 分别为可口可乐和百事可乐的最优产量曲线。在 Q 1 上，对给定的 q 2 ，可以把 Q 1 上的点的横坐标即为可口可乐的最优产量 q 1 ^，而 Q 2 表示给定一个 q 1 ，其对应 Q 2 上的点的纵坐标则是百事可乐的最优产量 q 2 ^。

2

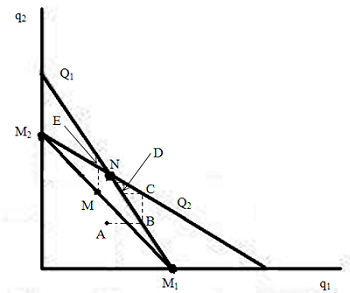
　　那两家公司的产量策略会对应于图上的哪一点呢？那就是两条最佳策略线的交点 N，因为这里表示双方同时达到最佳策略。假设一开始两家的策略对应于图上任意一点，比如 A，如果可口可乐最先意识到将策略按最佳策略线 Q 1 调整时自己获利最大，它就会立刻改变产量，策略从点 A 移动到 B，这时，百事可乐自然知道需要把策略移到自己的最佳策略线 Q 2 上，因此策略从 B 移到 C。为了让策略回到 Q 1 上，可口可乐选择降低自己的产量，策略又从 C 移动到 D。从图上可以看见，由于双方都希望策略位于自己的最佳策略线，最后的结果是策略趋向于 Q 1 和 Q 2 的交点 N。

　　而图中的 M 1 表示可口可乐垄断市场，百事可乐一点都不生产。根据经济学的一点知识，完全垄断是所有市场形式中利润最高的。类似的， M 2 表示百事可乐完全垄断。那么， M 1 和 M 2 的中点 M 表示是什么呢？这就好比把可口可乐和百事合并成一个公司，实施垄断经营，然后把利润平分。这样每个公司得到的利润是最大的，高于 N 点。然而，要说服大家离开N而合作到达 M 是很困难的。一方面，如果一家不讲信用，就可以通过设置自己的产量获得更大的利润，而对手则蒙受损失。另外，两家保持垄断会吸引新的厂商进入市场，从而导致垄断破裂。

　　然而，脱离 N 点也并非不可能，至少百事和可口可乐就做到了。一方面，两家公司其实一直在重复这个博弈，这使得脱离纳什均衡选择收益更大的策略更有可能。如果一方违反默契，可能造成对方的报复，进而损失更多的利益。另外，可乐生产尽管不是什么高科技，但大家早就对这两家公司有了品牌认同感，新的公司想要抢占市场还是很困难的。